Table Of Content

We should partition our study participants into gender, age, and exercise groups and then randomly assign the treatment (placebo vs drug) within the group. This will ensure that we do not have a gender, age, and exercise group that has all placebo observations. Once the participants are placed into blocks based on the blocking variable, we would carry out the experiment to examine the effect of cell phone use (yes vs. no) on driving ability. Those in each block will be randomly assigned into either treatment conditions of the independent variable, cell phone use (yes vs. no). As we carry out the study, participants' driving ability will be assessed.
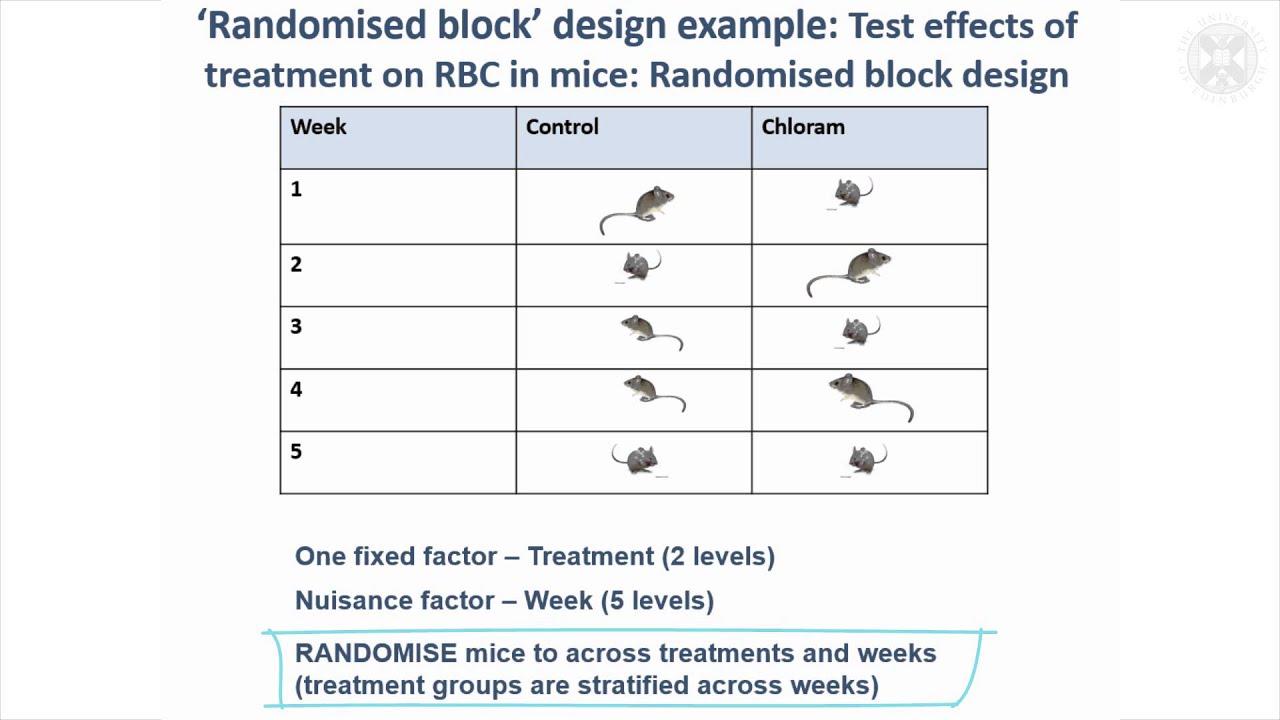
Comparing the CRD to the RCBD
One issue that makes this issue confusing for students is that most texts get lazy and don’t define the blocks, plots, and sub-plots when there are no replicates in a particular level. To each set of 3 plots, we’ll randomly assign the 3 varieties, and to each set of subplots, we’ll assign the fertilizers. By randomly assigning individuals to either the new diet or the standard diet, researchers can maximize the chances that the overall level of discipline of individuals between the two groups is roughly equal. However, a nuisance variable that will likely cause variation is gender. It’s likely that the gender of an individual will effect the amount of weight they’ll lose, regardless of whether the new diet works or not. There are two additional assumptions unique to randomized block ANOVA.
2.6 Replication Within Blocks
Contrasts are defined exactly as for our previous designs, but their estimation is based only on the intra-block information if the estimated marginal means are calculated from the ANOVA model. Estimates and confidence intervals then differ between ANOVA and linear mixed model results, and the latter should be preferred. For our example, we calculate three contrasts comparing each drug respectively their average to placebo. The results are given in Table 7.4, and demonstrate the differences in degrees of freedom and precision between the two underlying models. Properties non-specific to the experimental units include (i) batches of chemicals used for the experimental unit; (ii) device used for measurements; or (iii) date in multi-day experiments. These are often necessary to account for systematic differences from the logistics of the experiment (such as batch effects); they also increase the generalizability of inferences due to the broader experimental conditions.
2.4 Evaluating and Choosing a Blocking Factor
If we conduct this as a blocked experiment, we would assign all four tips to the same test specimen, randomly assigned to be tested on a different location on the specimen. Since each treatment occurs once in each block, the number of test specimens is the number of replicates. We have four different varieties of rice; varieties A, B, C, and D. So, imagine each of these blocks as a rice field or patty on a farm somewhere. These blocks are just different patches of land, and each block is partitioned into four plots. Then we randomly assign which variety goes into which plot in each block.
In each field, we will plant all three varieties so that we can tell the difference between varieties without the block effect of field confounding our inference. Statology Study is the ultimate online statistics study guide that helps you study and practice all of the core concepts taught in any elementary statistics course and makes your life so much easier as a student. The nuisance factor they are concerned with is "furnace run" since it is known that each furnace run differs from the last and impacts many process parameters.
Randomization, Blocking, and Re-Randomization by Leihua Ye, PhD - Towards Data Science
Randomization, Blocking, and Re-Randomization by Leihua Ye, PhD.
Posted: Sun, 21 Nov 2021 08:00:00 GMT [source]
While it is true randomized block design could be more powerful than single-factor between-subjects randomized design, this comes with an important condition. As you have seen from the procedure described above, it shouldn't come as a surprise that it is very difficult to include many blocking variables. Also, as the number of blocking variables increases, we need to create more blocks. Each block has to have a sufficient group size for statistical analysis, therefore, the sample size can increase rather quickly. The selection of blocking variables should be based on previous literature. An example layout of this design is shown in Figure 7.14A, where the two blocking factors are given as rows and columns.
Statology Study
The third case, where the replicates are different factories, can also provide a comparison of the factories. The fact that you are replicating Latin Squares does allow you to estimate some interactions that you can't estimate from a single Latin Square. If we added a treatment by factory interaction term, for instance, this would be a meaningful term in the model, and would inform the researcher whether the same protocol is best (or not) for all the factories.
Can MANOVA be performed on data with RCBD? - ResearchGate
Can MANOVA be performed on data with RCBD?.
Posted: Thu, 09 May 2013 07:00:00 GMT [source]
No Blocking Variable vs. Having a Blocking Variable

Randomization is our insurance against a systematic bias due to a nuisance factor. A special case is the so-calledLatin Square design where we have two blockfactors and one treatment factor having \(g\) levels each (yes, all of them!).Hence, this is a very restrictive assumption. In a Latin Square design, eachtreatment (Latin letters) appears exactly once in each row and once ineach column. A Latin Square design blocks on both rows and columnssimultaneously.
For example, we might be concerned about the effect of litters on our drug comparisons, but suspect that the position of the cage in the rack also affects the observations. The latin square design removes both between-litter and between-cage variation from the drug comparisons. For three drugs, this design requires three litters of three mice each, and three cages. Crossing litters and cages results in one mouse per litter in each cage.
We will try to account for these nuisance factors in our model and analysis. Second, the blocking variable cannot interact with the independent variable. In the example above, the cell phone use treatment (yes vs. no) cannot interact with driving experience. This means the effect of cell phone use treatment (yes vs. no) on the dependent variable, driving ability, should not be influenced by the level of driving experience (seasoned, intermediate, inexperienced). In other words, the impact of cell phone use treatment (yes vs. no) on the dependent variable should be similar regardless of the level of driving experience.
We can use two blocking factors with a balanced incomplete block design to reduce the required number of levels for one of the two blocking factors. These designs are called Youden squares and only use a fraction of the treatment levels in each column (resp. row) and the full set of treatments in each row (resp. column). The idea was first proposed by Youden for studying inoculation of tobacco plants against the mosaic virus (Youden 1937), and his experiment layout is shown in Figure 7.16. The use of blocking in experimental design has an evolving history that spans multiple disciplines. The foundational concepts of blocking date back to the early 20th century with statisticians like Ronald A. Fisher. His work in developing analysis of variance (ANOVA) set the groundwork for grouping experimental units to control for extraneous variables.
The blocked way to run this experiment, assuming you can convince manufacturing to let you put four experimental wafers in a furnace run, would be to put four wafers with different dosages in each of three furnace runs. The only randomization would be choosing which of the three wafers with dosage 1 would go into furnace run 1, and similarly for the wafers with dosages 2, 3 and 4. The undergraduate major at Berkeley provides a systematic and thorough grounding in applied and theoretical statistics as well as probability. The quality and dedication of the teaching staff and faculty are extremely high. A major in Statistics from Berkeley is an excellent preparation for a career in science or industry, or for further academic study in a wide variety of fields.
If we carefully select the blocking factors, we can assume these interactions to be negligible and arrive at the much simpler experiment design in Figure 7.12D. Our experiment again uses 24 mice, with four litters per laboratory, and each litter is a block with one replicate per drug. The model specification is y ~ drug + Error(lab/litter) for an analysis of variance, and y ~ drug + (1|lab/litter) for a linear mixed model. As more than one litter is used per lab, the linear mixed model directly provides us with estimates of the between-lab and the between-litter (within lab) variance components. Since the two blocks are nested, the omnibus \(F\)-test and contrasts for Drug are calculated within each litter and then averaged over litters within labs. Crossing a unit factor with the treatment structure leads to a blocked design, where each treatment occurs in each level of the blocking factor.

No comments:
Post a Comment